Semana dos . Taller 1: Lenguaje algebraico Taller 2: Expresiones algebraicas Taller 3: Valor numérico

Febrero 2 al 6

Competencias a desarrollar:

Aprender que el lenguaje ordinario puede escribirse en lenguaje algebraico.

Identificar un monomio, binomio, trinomio y polinomio; así como las partes de un término algebraico, el grado absoluto, grado relativo de un término algebraico y de un polinomio.

Bibliografía:

https://www.geogebra.org/m/c6gPXezN

https://guao.org/sites/default/files/biblioteca/%C3%81lgebra%20de%20Baldor.pdf

 ¿Qué es el lenguaje algebraico? (definición simple)

Es una forma de escribir situaciones matemáticas usando letras, números y símbolos.
Las letras representan números que no conocemos todavía (variables).

Ejemplo:

“Un número más 5” → x + 5

Entendé bien las variables

• Letras como x, y, a representan números.

• No son misteriosas: solo reemplazan valores.

Ejemplo:

Si x = 3 → x + 2 = 5

Aprende a traducir palabras a símbolos

Esto es CLAVE en octavo.

Lenguaje común	Lenguaje algebraico
Un número	x
El doble de un número	2x
La mitad de un número	x ÷ 2
Un número más 7	x + 7
Un número menos 4	x − 4

 otros ejemplos: 

1️⃣ La tercera parte de un número
👉 $\dfrac{x}{3}$

2️⃣ El triple de un número
👉 $3x$

3️⃣ Un número disminuido en dos
👉 $x - 2$

4️⃣ Un número aumentado en dos
👉 $x + 2$

5️⃣ El cuadrado de la suma de dos cantidades
👉 $(a + b)^2$
⚠️ Ojo: no es $a^2 + b^2$

6️⃣ El doble de la suma de dos números
👉 $2(a + b)$

7️⃣ El cubo de un número disminuido en nueve
👉 $(x - 9)^3$

8️⃣ El doble de la suma de los cuadrados de p y q
👉 $2(p^2 + q^2)$

🔥 Tip clave:

• “la suma de” → va entre paréntesis

• “el cuadrado / cubo de” → afecta a todo lo que está dentro

TALLER N.º 1

Tema: Lenguaje algebraico

Instrucciones:
Traduce las siguientes expresiones del lenguaje común al lenguaje algebraico.

---

1. El triple de la suma de a y c.

2. La suma del cubo de x, y y z.

3. La raíz cúbica de la diferencia de x y z.

4. El cubo de c disminuido en cuatro.

5. El doble de la diferencia de los cuadrados de p y g.

6. El triple de la suma de los cubos de m y n.

7. Tres veces el cubo de x más el cuadrado de y.

8. La raíz cuadrada del cubo de la suma de a y b.

9. La tercera parte de la suma de los cubos de m y n.

10. Un número aumentado en dos es igual a diez.

11. Un número disminuido en ocho es igual a menos veinte.

12. El triple de un número disminuido en siete es igual a cincuenta y tres.

13. La mitad de un número aumentada en tres es igual a ocho.

14. La quinta parte de un número aumentada en dos es igual a seis.

15. El triple de un número dividido entre cuatro es igual a tres.

¿Qué es el álgebra?

El álgebra es una rama de las matemáticas que utiliza letras, números y símbolos para representar cantidades y resolver problemas, especialmente cuando no se conocen algunos valores.

Las letras se llaman variables y representan números que pueden cambiar o que no conocemos.

Ejemplo:
Si no sabemos qué número es, lo representamos con una letra:

$$x+3$$

¿Qué son las expresiones algebraicas?

Una expresión algebraica es una combinación de números, letras y operaciones matemáticas (suma, resta, multiplicación, división, potencias) que representa una cantidad, pero no tiene signo igual.

Las expresiones algebraicas se usan para traducir frases escritas en palabras al lenguaje matemático.

Lenguaje algebraico. Ver videos:  clic clic

Ejemplos de expresiones algebraicas:

• $x + 5$

• $x$

• 
  

Diferencia importante:

• Expresión algebraica: no se resuelve, solo representa
  Ejemplo: $x + 2$
  

• Ecuación: tiene signo igual y se puede resolver
  Ejemplo: $3x+2=11$
  

Álgebra   Ver video: clic

La palabra álgebra proviene del vocablo Árabe " Al jarb" que significa ciencia de la transformación y la reducción, del paso y del arreglo, del intercambio y el manejo.

Se emplea para sintetizar los diferentes conceptos de ciencias como la física, la geometría analítica, la química y el cálculo.

Proporciona también una serie de instrucciones útiles para obtener resultados en el menor tiempo posible, de una forma ordenada y práctica, utilizando un código ordenado de letras, números y signos de operación y relación.

A) Literales ( letras )

B) Números

C) Operación ( el por, el dividido, potenciación y radicación)

D) Relación ( mayor que, menor que e igual a )

E) Agrupación ( paréntesis, corchetes y llaves )

Expresión algebraica ver video clic

Una expresión algebraica es una combinación de letras, números y signos de operaciones. Las letras suelen representar cantidades desconocidas y se denominan variables o incógnitas.

Las expresiones algebraicas nos permiten traducir al lenguaje matemático expresiones del lenguaje habitual.

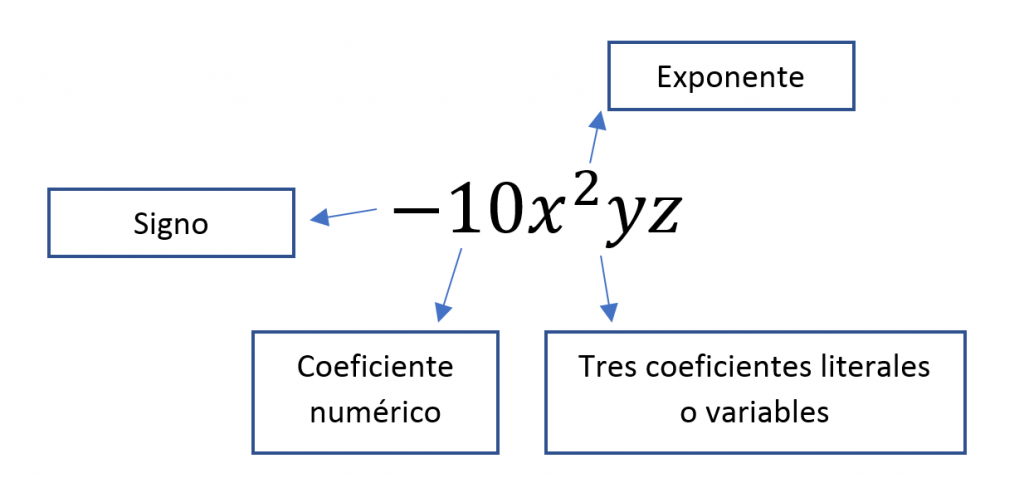
Término algebraico

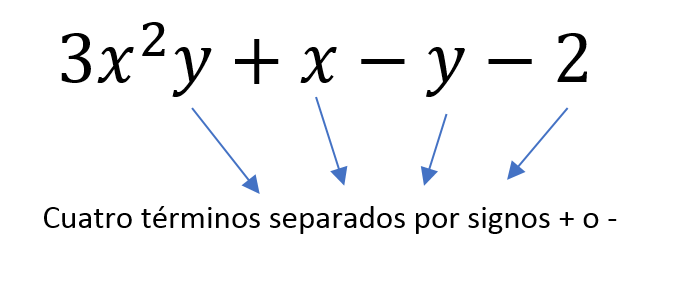
En álgebra, un término algebraico, es un solo número o variable, o números y variables multiplicados entre sí.

Los términos están separados por los signos “+ o –“.

En todo término algebraico pueden distinguirse cuatro elementos: el signo, el coeficiente, la parte literal y el grado.

Ejemplo:

Un Término consta de dos partes: coeficiente y factor literal.

Coeficiente: Es el número que va delante de las letras (si no lleva ninguna cifra, recuerda que lleva el 1).

Factor Literal: Es la compuesta por letras con sus exponentes, si los tienen.

El grado de un Término Algebraico es el mayor exponente de término algebraico.

Grado Absoluto de un Término Algebraico  ver video  clic

El grado absoluto de un término algebraico es la suma de todos los exponentes de las variables algebraicas.

El grado absoluto de un término algebraico se obtiene sumando todos los exponentes de las variables.

Ejemplo:

7a5b4c7

Grado = 5 + 4 + 7

Grado = 16

Grado Relativo de un Término Algebraico

El grado relativo es el valor del exponente de cada variable.

Ejemplo:

7a5b4c7

Grado de a = 5

Grado de b = 4

Grado de c = 7

Tipos de expresiones algebraicas  ver video: clic

Monomio                  Binomio                                 Trinomio

7y                             3x 2x + 4                                X2 + x + 5

Monomio: Se llama monomio a la expresión algebraica que tiene un solo término. Ejemplos de expresiones algebraicas de un solo término:

Son monomios: 5x2 , 2xy3, -4xy2z4, x3, 3x

El número que multiplica a las letras se llama coeficiente y las letras parte literal.

Grado de un monomio

Se llama grado de un monomio al número de factores que forman la parte literal, se obtiene sumando los exponentes de las variables.

Binomio: Se llama binomio a la expresión algebraica que tiene dos términos. Ejemplos de expresiones algebraicas de dos términos:

               2) 4x2 − 25            3) 9x2 + 27x                   4) a3 − b3

Trinomio: Se llama trinomio a la expresión algebraica que tiene tres términos. Ejemplo:

Polinomio: Expresión algebraica de más de 3 términos.

► El grado de un polinomio es el mayor de los grados de los monomios que los forman.

► Llamamos coeficiente principal al coeficiente del monomio de mayor grado.

► El término independiente el monomio que tiene grado cero, es decir, el que no tiene variables.

Taller 2: Expresiones algebraicas

1. Para cada uno de los siguientes términos algebraicos, determine el grado absoluto del término y el grado relativo con relación a cada letra de los términos.

       

2. Identifique el signo, coeficiente numérico, parte literal, exponente de la parte literal, operador y el grado absoluto de cada uno de los siguientes monomios:

3. Determine el grado y clasifica según el número de términos, nombre de  las siguientes expresiones algebraicas 8 si es monomio, binomio, trinomio o polinomio)

4. Escriba tres términos semejantes de cada uno de los siguientes términos algebraicos:

5. En el siguiente cuadro, colorea del mismo color los términos semejantes: 

TALLER  3: VALOR NUMÉRICO (sin terminar de digitar)

Calcula el valor numérico de las expresiones algebraicas siguientes, considerando:

SEMANA UNO 2026

OBJETIVO:

Determinar las pautas de trabajo y evaluativas durando el año 2026

Página a la que deben entrar los estudiantes:

http: //www.iemutismedellin.edu.co

• Oración y saludo de bienvenida.
• Presentación de los estudiantes y docente.
• Organización de listas.
• Conocimiento del objetivo general del área, competencias, indicadores de desempeño, sistema de evaluación, metodología de trabajo para el año y temas a trabajar el primer período.
• Información acerca de la forma de trabajo durante el año 2026
• Procesos evaluativos dentro del área para 2026
• Según el SIE  de la Institución Educativa José Celestino Mutis, se tendrá en cuenta:

 A)Participación en clase (trabajo en clase individual y en equipo, exposiciones, consultas, sustentaciones, ensayos, conversatorios, diálogos).El seguimiento tendrá un valor del 70%.

 B) Construcciones geométricas sencillas.

 C) Tareas, exámenes orales y escritos, mapas conceptuales y mentales.

 D)Carteleras, análisis de videos(cada semana el estudiante debe observar los videos y hacer un pequeño resumen del mismo que será comentado y calificado en clase)

 E)  La autoevaluación se realizará acorde a las pautas establecidas por el colegio, al final del período, con un valor del 10%

F) El examen final del período(tipo prueba saber) tendrá un valor del 20%

G) Se realizará coevaluación y heteroevaluación.

H) Cada clase se evaluará los temas de la clase anterior y los talleres que se realizaren, sólo tendrán como fin afianzar el aprendizaje de los temas tratados para que los estudiantes puedan sustentar a la clase siguiente.

Aspectos significativos de la autoevaluación

	Siempre	Casi Siempre	Algunas veces	Nunca
1.      Amplío los conceptos básicos del área, a través de diferentes fuentes y medios en tiempo extra clase
2.      Empleo saberes adquiridos en la clase para aplicarlos en mi quehacer diario
3.      Evidencio una actitud proactiva y respetuosa frente al desarrollo de las diferentes clases
4.      Cumplo con los compromisos y responsabilidad a nivel académico
5.      Participo activamente en el desarrollo de las diferentes actividades de clase
6.      Asisto a clases y eventos institucionales puntualmente
7.      Tengo capacidad de escucha y respeto por la diferencia
8.      Soy responsable en la realización y entrega puntual de los trabajos

 La coevaluación: Es el proceso de valoración conjunta que realizan todos los estudiantes  sobre la actuación del grupo, teniendo en cuenta los criterios de evaluación ya establecidos. Se  cuando esté finalizando cada período académico.

La heteroevaluación: Consiste en que el profesor evalúa a cada estudiante, su trabajo, su actitud, responsabilidad, rendimiento, aprendizaje, etc.

 Autoevaluación de fin de período: Permite a cada estudiante emitir juicios de valor sobre sí mismo en función de los criterios de evaluación o indicadores que se les haya dado a conocer al comienzo del año.

Evaluación de fin de período: se realiza cada fin de período y tiene un valor del 20%.

Presentación de actividades de recuperación : Se hacen cada fin de período una vez el acudiente del estudiante, haya recibido el boletín de calificaciones. tendrá dos semanas de tiempo para realizarla. 
Consta de:

• Ponerse al día en su cuaderno en todos los conceptos consignados en las clases.
• Realizar y /o corregir todos los talleres realizados durante el período.
• Desarrollar un taller de refuerzo de logros que deberá reclamarle al docente inmediatamente después de  la entrega de boletín de calificaciones.
• Sustentar el taller asignado a través de una evaluación escrita, el cual debe aprobar con una nota mínima de 3.0 ( tres cero).

NOTA: SI EL ESTUDIANTE NO CUMPLE CON LOS CUATRO ASPECTOS ANTERIORMENTE MENCIONADOS, NO RECUPERA LOS LOGROS PENDIENTES.

BIBLIOGRAFÍA:

http://132.248.164.227/publicaciones/docs/apuntes_matematicas/02.%20Sistemas%20de%20Numeracion.pdf

Conocimientos básicos a estudiar en el 2026, los cuales se relacionan con procesos específicos que desarrollan el pensamiento matemático y los sistemas propios del área.

Estos son:

• Pensamiento numérico y sistemas numéricos. El énfasis en este sistema se da a partir del desarrollo del pensamiento numérico que incluye el sentido operacional, los conceptos, las relaciones, las propiedades, los problemas y los procedimientos.

• Pensamiento espacial y sistemas geométricos. El componente geométrico permite a los estudiantes examinar y analizar las propiedades de los espacios bidimensional y tridimensional, así como las formas y figuras geométricas que se hallan en ellos.

• Pensamiento métrico y sistemas de medidas. El desarrollo de este componente da como resultado la comprensión, por parte del estudiante, de los atributos mensurables de los objetos y del tiempo.

• Pensamiento aleatorio y sistema de datos. Los fenómenos aleatorios son ordenados por la estadística y la probabilidad.

• Pensamiento variacional y los sistemas algebraicos y analíticos.

SEMANA TRECE---IRRACIONALES EN LA RECTA NUMÉRICA

11 AL 15   DEABRIL

DECIMAL PERIÓDICO PURO, PERIÓDICO MIXTO, DECIMAL EXACTO---EJERCICIOS

VER ENLACE  Y HACER LOS EJERCICIOS  http://contenidosdigitales.ulp.edu.ar/exe/matematica1/actividad_33.html

QUÉ FRACCIÓN SE HA REPRESENTADO EN CADA CASO?

VER Y RESOLVER ENLACE http://contenidosdigitales.ulp.edu.ar/exe/matematica1/actividad_43.html

USO DE LOS NÚMEROS RACIONALES

VER ENLACE http://contenidosdigitales.ulp.edu.ar/exe/matematica1/usos_de_los_nmeros_racionales.html

ACTIVIDADES CON RACIONALES

RESOLVER LOS EJERCICIOS PRESENTADOS EN EL SIGUIENTE ENLACE  http://contenidosdigitales.ulp.edu.ar/exe/matematica1/actividades4.html

EVALUACIÓN, VE AL ENLACEhttps://www.thatquiz.org/es/previewtest?A/F/F/Z/71UV1434290825

Números Irracionales "I" y representación en la recta numérica.

El concepto de números irracionales proviene de la Escuela Pitagórica, que descubrió la existencia de números irracionales, es decir que no eran enteros ni racionales como fracciones. Esta escuela, los llamó en primer lugar números inconmensurables.

Todo número racional"Q" se puede representar mediante una expresión decimal que puede ser exacta, periódica pura o periódica mixta.

Las expresiones periódica puras o mixtas, tienen un número infinito de cifras decimales que se repiten periódicamente.

Ejemplos de decimales periódicos:

a) 0,333...                         d) 21, 100100100...

b) 0,31272727...               e) 0,415415...

c) 1,4565656...                 f) 1,325325...

 Todo número racional se le puede hacer corresponder un punto en la recta, pero el conjunto "Q no completa la recta.

 Si observamos, aún quedan puntos a los cuales no se les puede asignar un número racional. Esos puntos corresponden a números irracionales.

¿Qué son números irracionales? 

Son números que poseen infinitas cifras decimales no periódicas, que por lo tanto no pueden ser expresados como fracciones.

Expresiones como:

 0,13579111315...; 0,1011121617...; -5,13579111315...;3,48121620...; 5, 17131924...; etc. donde las infinitas cifras decimales que poseen no se repiten periódicamente, se llaman irracionales: Otros ejemplos son: √2, √3, √5, √6, √7, √8, √10,etc.

1).

no puede representar un número racional.

2). El número irracional más conocido es , que se define como la relación entre la longitud de la circunferencia y su diámetro.

 = 3.141592653589..

Para distinguir los números irracionales de los racionales, debemos tomar en cuenta que los números racionales si se pueden escribir de manera fraccionada o racional, por ejemplo: 18/5 que es igual a 3,6 por lo tanto es un número racional a diferencia de la raíz cuadrada de dos en cuyo resultado se obtienen infinito número de cifras decimales, y su fraccionamiento resulta imposible.

Otros números irracionales son:

1). El número e aparece en procesos de crecimiento, en la desintegración radiactiva, en la fórmula de la catenaria, que es la curva que podemos apreciar en los tendidos eléctricos.

e = 2.718281828459...

2). El número áureo, , utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.

Otros de números irracionales:

1. √31 = 5.5677643628300219221194712989185…

2. √999 = 31.606961258558216545204213985699…

3. √2 = 1. 4142135623730950488016887242096980785696…

4. √3 = 1.7320508075688772935274463415059…

5. π = 3,14159265358979323846…

6. φ = 1.618033988749894848204586834…

7. El número e (el número de Euler) 2,7182818284590452353602874713527…

8. √5 = 2.2360679774997896964091736687313…

9. √7 = 2.6457513110645905905016157536393…

10. √11 = 3.3166247903553998491149327366707…

11. √13 = 3.6055512754639892931192212674705…

12. √122 = 11.045361017187260774210913843344…

13. √15 = 3.8729833462074168851792653997824…

14. √17 = 4.1231056256176605498214098559741…

15. √21 = 4.582575694955840006588047193728…

16. √22 = 4.6904157598234295545656301135445…

17. √23 = 4.7958315233127195415974380641627…

18. √101 = 10.04987562112089027021926491276…

19. √500 = 22.360679774997896964091736687313…

20. √999 = 31.606961258558216545204213985699…

21. √1000 = 31.622776601683793319988935444327…

22. √1001 = 31.638584039112749143106291584801…

23. √9 = 2.080083830519041145300568243579…

24. √6 =1.817120592832139658891211756373…

25. √5 = 1.7099759466766969893531088725439…

26. √7 = 1,9129311827723891011991168395488…

27. √3 = 1,4422495703074083823216383107801…

28. √12 = 2,2894284851066637356160844238794…

29. √13 = 2,3513346877207574895000163399569…

30. √33 = 3,2075343299958264875525151717195…

Representación de los números irracionales.

¿Cómo se puede representar, por ejemplo,  √2 ?

√2 = 1,414...,es decir, 1< √2 < 2

Para representarlo debemos seguir los siguientes pasos:

Paso 1: construir sobre la recta numérica un triángulo rectángulo de dimensiones 1cm de ancho 1cm de alto y vamos a llamar x a la hipotenusa.

Paso 2: aplicar el Teorema de Pitágoras como sigue:

Paso 3: Ya sabemos que el valor de la hipotenusa tiene como valor raíz de 2, luego con la ayuda de un compás podemos representar en la recta el valor de √2 de la siguiente manera.  Con tu compás toma la dimensión de la hipotenusa, que en este caso es √2, y toma como centro el cero. Luego trazas un arco de circunferencia y el punto de corte con la recta  numérica será el valor de raiz de 2 (longitud desde el punto cero al punto P).

Con la ayuda de un compás podemos representar exactamente √2 en la recta numérica. 

Sabemos que √2  es un número irracional, por lo tanto, el punto P de la recta no puede estar ocupado por ningún otro número irracional.

¿Cómo representar Raíz de tres ( √3 ) en la recta numérica?

A) Sobre la recta numérica, a partir de cero, se dibuja un rectángulo de lado (base) igual a √2 y altura 1.

B) Trazamos una diagonal dsde cero hasta el vértice opuesto, formándose dos triángulos rectángulos, donde conocemos los catetos, entonces hallamos la hipotenusa.

Luego aplicamos el teorema de pitágoras y hallamos el valor de la hipotenusa, así:

a²= b²+c²

a²= (1)²+ (1)²

a²= 1+1

a²= 2

luego:  √a²= √2    entonces:

a= √2

Por lo tanto, la diagonal(hipotenusa) es igual a √2

                  ____b=√2______

  

Taller nº ____

Ubicar en la recta numérica √3, √5, √6, √7, √8, √10 y aplicar a cada una de ellas el teorema de Pitágoras.

notacion cientifica

Tomado de: https://www.colegiocolonos.cl/upload/textos/aprendizaje-remoto-20-medios-3184d7ab8c358f5a198cbde93131497c.pdf

TALLER   Tema: Números irracionales “I”  

             

1. Encuentre la característica de la parte infinita y explique porqué es un numero irracional

A. 5, 510152025302540455055...__________________________________

B. 9, 9182736455463728190______________________________________

C. 8, 8162432404856647280______________________________________

D. 3, 369121518243240485664...___________________________________

E. 2,22468101214161820222426...__________________________________

2. De las siguientes expresiones señale cuáles representan números racionales e irracionales.

a) 0,25                               b) 0,43636                           c)1/3     

d) 3/8                                 e) 0,3333                             f) 1,03737    

9) 5/3    

3. Sobre la recta numérica grafique los siguientes números irracionales:                                                       

a) -     b) -      c) 1+      d) 2 +    e)  + 1  f) 2   g) -   h)  – 1

_________________________________________________________________

4. Dadas las siguientes afirmaciones, indique cuáles son verdaderas y cuáles son falsas.

a) Ningún número entero es racional (   )          b) Algún número entero es racional (   )

c) Ningún número irracional es entero (   )       d) Todo número natural es entero (   )

e) Al menos un número irracional es racional (   ) e) Ningún número irracional es entero (   )

5. Utilizando el teorema de Pitágoras, encuentre la medida de la magnitud que se señala.

                                                 

       4   =        ¿                                                                            3        3                              100                       36

                                  3                                                 9                                                               ¿

Z

6. Dado el siguiente diagrama de Venn donde se representa a relación de contenencia entre los conjuntos numéricos, ubique en la región que corresponda, cada uno de los siguientes números:

Z

N

                   Q

                                                                                

__________________________________________________________________________________________________

TALLER 2 ---------NOTACIÓN CIENTÍFICA

2. Efectúe las operaciones de los números escritos en notación científica. Exprese el resultado en notación científica:

a)      (3,456 x 10⁸) x (6,934 x 10³)       b)   (5,6 x 10^-3) x (8,99 x 10⁷)      c) (6,9 x 10⁹) ÷ (8,3 x 10^-3)

3. Escriba en notación científica:           a) 0,000 000 35      b) 0,3 . 10⁵      c) 0,1 . 10^-3          d) 12,5 . 10⁴  

4.   Escriba en notación científica los siguientes datos correspondientes a la tierra:

a) Masa:  6 000 000 000 000 000 000 000 000 Kg            b) Radio: 6 400 000 Km

c) Superficie: 500 000 000 m                                                d) volumen: 1. 083 000 000 000 Km³

5. Exprese en notación científica:   a) velocidad de la luz 300 .000 m/seg.        b) Radio terrestre: 6 370 000 metros

c) Edad de la tierra: 4 500 000 000 años.     d) Radio de la luna: 1 700 000 metros.    e) Desaparición de los dinosaurios: 65. 000.000 años     f) Medida del virus de la gripe: 0, 000 000 120 metros  g) tiempo transcurrido desde que los primeros animales habitaron el mundo sobre la tierra seca: 12 000 000 000 000 000 segundos  h) Tiempo que tarda un rayo de luz en atravesar una ventana 1/ 100 000 000 000 segundos

4. Escriba en notación científica:

a) 0,000 000 35              b) 12, 5 . 10⁴          c) 0,1 x 10^-3        
d) 0,03 . 10⁵

   

5. Complete: 

a) 3. 10⁶  . 10⁸       b)  2,5 x 10¹²  = ______ . 10⁸      c) 0, 000 007 = 7   . ________

d) 0 , 1  . 10^-7   = _________ . 10 ^-10

6. El radio de marte es de 3, 4 . 10⁶ m.  Para calcular el diámetro, se multiplica el radio por 2. ¿Cuál de los siguientes valores corresponde al diámetro?

a)    D= 2. 3, 4  . 10⁶   m = 6 ,8 . 10⁶ m        c) D= 2. 3, 4 . 10⁶ m = 3, 4 . 101² m

b)   D= 2  . 3,  4  . 10⁶ m = 6, 8 . 101² m   

7. Complete:

a) 3 . 10^-5 m = 0,3 . 10^-3     _______________     

b) 1, 2 . 10^-3  Km = 0,12 m    

c)  0,001 . 10^-6 m = ___________ . 10^-9  Km      

d)  10⁵ m = ________ . 10³  m

e) 8, 12 . 10³ m = 0, 812 . 10²     _______ 

8. Escriba en notación científica los siguientes datos con respecto al sol:

A. Diámetro del sol 1360000 Km

B. Volumen del sol1400000000000000000000 Km

9. Escriba en notación científica:

A. 0,00000035

B. 0, 0 3 . 105

C. 0, 1 . 10-3

D. 12, 5 . 104

E. 83000000

10. Escriba los siguientes volúmenes en notación científica:

A. Volumen de júpiter 14. 1014 Km3

B. Volumen de marte 0,17. 1021 m3

C. Volumen de Urano 5700. 1010 m3

11. El radio de marte es de 3, 4 . 106 m; para calcular el diámetro se multiplica el radio por dos. ¿Cuál de los siguientes valores corresponde al diámetro de marte? ( si no lo encuentras, búscalo):

A. D= 2 . 3, 4. 106m = 6, 8. 106 m

B. D= 2. 3, 4. 106 = 6, 8. 1012 m

C. D=2 . 3, 4. 106 m = 3, 4. 1012 m

13. Escriba en forma abreviada:
 a) 0, 000 000 9                          b) 0, 000 000 045     

 c) 0,00 000 000 000 001 7               d) 0, 000 000 000 24