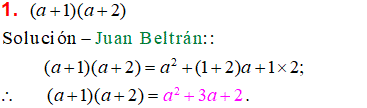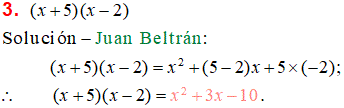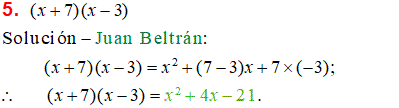Taller 20:Producto de la forma ( 𝑥 ± 𝑎 ) ( 𝑥 ± 𝑏 ) (x±a)(x±b) y Producto de la suma por la diferencia de dos cantidades.

3. Producto de la suma por la diferencia de dos cantidades o binomio conjugado: (a + b) ( a - b )

Ver enlace https://www.algebra.jcbmat.com/id1140.htm

El producto de la suma por la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, MENOS el cuadrado de la segunda cantidad.

 Ejemplo 1 :

Ejemplo 2: 

                            ( x + 9 ) ( x – 9 ) = x² - 81

Ejemplo 3:

Producto de dos binomios de la forma (x + a)(x + b)

P r o c e d i m i e n t o :

1.  El desarrollo del producto da un trinomio

2.  El primer término será el cuadrado del primer término de los binomios (igual en ambos)

3.  El segundo término será el producto de la suma de los términos distintos por el término común de los binomios

4.  El tercer término será el producto de los términos distintos (cada uno con su respectivo signo)  

Ejemplos: 

 1

 2

 3

 4

 5

 6

Tomado de : https://www.algebra.jcbmat.com/id1142.htm#google_vignette

 

Semana 27-28-29-30 Taller 19 Tema: Cuadrado de la suma y cuadrado de la diferencia de dos cantidades

 Productos notables

Son ciertos productos que cumplen reglas fijas y cuyo resultado puede ser escrito sin necesidad de verificar la multiplicación.

CASOS:

1. El cuadrado de la suma de dos cantidades: O  binomio al cuadrado:  (a +b)² 

^2. Cuadrado de la diferencia de dos cantidades o binomio al cuadrado: (a - b)² 

^3. Producto de la suma de dos cantidades por la diferencia  dos cantidades  

(a + b) ( a - b )

4. Cubo de la suma de dos cantidades o binomio al cubo: (a +b)³ 

^5.  Cubo de la diferencia de dos cantidades o binomio al cubo: (a - b)³  

^{6. Triángulo de Pascal}

^{7. Producto de la forma x más  menos a, por x más o menos b}

                                                                                       

1. El cuadrado de la suma de dos cantidades: O  binomio al cuadrado:  (a+b)² 

Ver enlace: https://www.algebra.jcbmat.com/id1138.htm

Es igual al cuadrado de la primera cantidad, MÁS el doble de la primera cantidad multiplicada por la segunda, MÁS el cuadrado de la segunda cantidad.

Ejemplo 1 :

  Demostración:

Ejemplo 2 :

                        (3a + 5b )²             = (3 a) ²    + 2 ( 3 a ) ( 5 b )   + ( 5 b ) ²

                                                    =     9 a ²   +       2 .15 a b      + 25 b ²

                                                               =     9 a ²   +        30 a b         + 25 b ²   R//

2. Cuadrado de la diferencia de dos cantidades: (a - b)² 

Ver enlace https://www.algebra.jcbmat.com/id1139.htm

                                             

El cuadrado de la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, MENOS el doble de la primera cantidad multiplicada por la segunda, MÁS el cuadrado de la segunda cantidad. 

Ejemplo:

Demostración:

3. Producto de la suma por la diferencia de dos cantidades o binomio conjugado: (a + b) ( a - b )

Ver enlace https://www.algebra.jcbmat.com/id1140.htm

El producto de la suma por la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, MENOS el cuadrado de la segunda cantidad.

 Ejemplo 1 :

Ejemplo 2: 

                            ( x + 9 ) ( x – 9 ) = x² - 81

Ejemplo 3:

4. Cubo de la suma de dos cantidades o binomio al cubo: (a+b)³   

Ver enlace: https://www.algebra.jcbmat.com/id1164.htm

                    

Es igual al cubo de la primera cantidad MÁS el triple  del cuadrado de la primera cantidad por la segunda, MÁS el triple de  la primera cantidad por el cuadrado de la segunda, MÁS  el cubo de la segunda.

VER VIDEO: CLIC

 Ejemplos:

5. Cubo de la diferencia de dos cantidades o binomio al cubo: 

(a - b)³   

^{Ver enlace: https://www.algebra.jcbmat.com/id1164.htm}

Es igual al cubo de la primera cantidad MENOS el triple  del cuadrado de la primera cantidad por la segunda, MÁS el triple de  la primera cantidad por el cuadrado de la segunda, MENOS  el cubo de la segunda. Ejemplos:

VER VIDEOS: CLIC

Videos de productos notables:

Suma por diferencia de dos cantidades: clic

Binomio al cuadrado: clic

Binomio al cubo: clic

Producto de la forma (x+ a)(x+ b): clic

Cuadrado de la suma de dos cantidades: clic

Cuadrado de la diferencia de dos cantidades: clic

Taller 19 Nota: El taller 18 está en la semana 31.

Tema: Cuadrado de la suma y cuadrado de la diferencia de dos cantidades

Objetivo: Aplicar las fórmulas (a+b)² = a² + 2ab + b² y (a-b)² = a² - 2ab + b²

Indicaciones

Lea las fórmulas anteriores y resuelva los siguientes ejercicios aplicando la fórmula correspondiente (cuadrado de la suma o cuadrado de la diferencia). Escriba cada paso con claridad.

Nota: El taller 18 está en la semana 31.

SEMANA 26: taller 17: MULTIPLICACION DE POLINOMIOS

 

Tema: Multiplicación de Polinomios

---

✅ OBJETIVO

Comprender y aplicar la multiplicación de polinomios mediante el método distributivo, organizando los términos semejantes de forma ordenada.

---

✅ DBA

Reconoce y aplica las propiedades algebraicas en la multiplicación de polinomios, simplificando mediante la reducción de términos semejantes.

Producto de polinomios

1. Se ordena el polinomio en forma ascendente o descendente.

2. Se halla el producto de cada término del multiplicador por cada uno de los términos del multiplicando, teniendo en cuenta la ley de los signos.

3. Se reducen términos semejantes si los hay.

Ejemplos: ver video clic

Efectuar los siguientes productos:

Ejemplo A)

Ejemplo B)

Ejemplos con multiplicación de polinomios con coeficiente fraccionario:

Multiplicación de polinomios con coeficiente fraccionario. Ver el video clic

TALLER 17

TEMA: Multiplicación de polinomios

Del algebra de A. Baldor en la página 72, ejercicio 44, los numerales 4,5,6. Resolverlos paso a paso y con procedimientos completos sin uso de calculadora ni de inteligencia artificial.

---

1. TEORÍA Y PASOS

1️⃣ Escribe los polinomios ordenados.
2️⃣ Multiplica cada término del primer polinomio por cada término del segundo.
3️⃣ Organiza uno debajo del otro, alineando términos semejantes.
4️⃣ Suma o resta los términos semejantes para obtener el resultado final.

✅ CONCLUSIÓN

• Al multiplicar polinomios, cada término del primero se multiplica por cada término del segundo.

• Se organizan en columnas para no confundir los términos.

• Luego se reducen términos semejantes para simplificar.

SEMANA 25 TALLER 16: MEDIDAS DE TENDENCIA CENTRAL: MEDIA ARITMÉTICA, MEDIANA Y MODA.

OTROS EJEMPLOS:

MEDIA  MODA MEDIANA

FORMA CORRECTA DE INTERPRETAR MODA, MEDIANA Y MEDIA ARITMÉTICA

EN LA MODA DIRÍAMOS: La edad con más frecuencia es 15 años. ( no podemos decir que la mayoría tienen 15 años, porque no son la mayoría, mira que de 9 estudiantes, 3 tienen 15 años, entonces digamos, que la edad con más frecuencia es 15 años.

EN LA MEDIA ARITMÉTICA, lo correcto es decir: El promedio de las edades del grupo de amigos es 15, 6 años.

PARA LA MEDIANA( es el dato del medio) decimos: El 50% de las personas es menor o igual a 15 años, o el 50% de los estudiantes es mayor o igual, tiene una edad mayor o igual a 15 años.

ESTADÍSTICA

TALLER 16 TEMA: Medidas de tendencia central.

VER VIDEO CÓMO INTERPRETAR MEDIA, MEDIANA Y MODA.CLIC

VER VIDEO CÓMO HALLAR MEDIA, MODA Y MEDIANACLIC

En el taller anterior haga la interpretación correcta de cada estudio estadístico, para ello vaya a los ejemplos del cuaderno.