SEMANA TRES: NÚMEROS Q--TALLER N° 1: JERARQUÍA DE LAS OPERACIONES, POLINOMIOS ARITMÉTICOS.

 FEBRERO 3 AL 7

Definición de los números racionales (Q)

Los números racionales son aquellos que se pueden expresar como el cociente de dos números enteros, es decir, como una fracción  a/b, donde a y b son números enteros y además b es distinto de cero.

El conjunto de los números racionales se representa con la letra Q. 

Los números racionales incluyen: Los números enteros (positivos y negativos), Los decimales, las fracciones. 

a: Enteros

b. En forma de fracción

c. En forma decimal

a. Enteros: todos los positivos, negativos y el cero.

a. En forma de fracción

• Los que se pueden escribir en forma a/b, siendo el numerador a y el denominador b números enteros con b ≠ 0

• Ejemplo: -3 = -3/1, los enteros también son racionales

  Fracciones equivalentes. Todas las fracciones que valen lo mismo. Fracciones equivalentes son aquellas fracciones que representan la misma cantidad aunque el numerador y el denominador sean diferentes.

¿Cómo sabemos si dos fracciones son equivalentes?

Lo son si los productos del numerador de una y el denominador de la otra son iguales, es decir, productos cruzados.

Vamos a ver unos ejemplos:

Comprobemos si 2/5 y 4/10 son equivalentes.

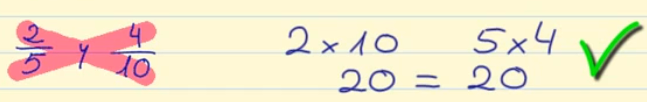
Para ello multiplicamos el numerados de una de las fracciones por el denominador de la otra.

2 x 10 = 20                     5 x 4 = 20

Como el resultado es el mismo, podemos decir que 2/5 y 4/10 sí son fracciones equivalentes.

¿Cómo podemos calcular fracciones equivalentes?

Por amplificación

Multiplicando numerador y denominador por el mismo número.

Por ejemplo, partiendo de la fracción 1/3 y multiplicando el numerador y el denominador por el mismo número, podemos obtener diferentes fracciones equivalentes.

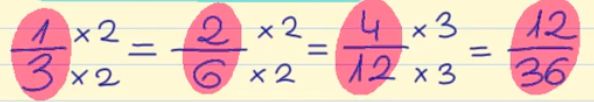
Si multiplicamos por 2:           1 x 2 = 2          3 x 2 = 6

por lo tanto la fracción 2/6 es equivalente a la fracción 1/3

Por simplificación

Dividiendo numerador y denominador por un divisor común de ambos.

Por ejemplo, 12/30 podemos dividir el numerador y el denominador entre 2, ya que tanto el numerador como el denominador son pares.

12 : 2 = 6          30 : 2 = 15

por lo tanto 6/15 es una fracción equivalente a 12/30

b. En forma decimal: La forma decimal puede ser de tres formas:

Decimal exacto, cuando la parte decimal tiene un número finito de cifras: 3,27.

Decimal periódico puro, cuando toda la parte decimal se repite indefinidamente: 3,2727272727…

Decimal periódico mixto, cuando no toda la parte decimal se repite: 3,2777777

Jerarquía de las operaciones

Ver video: clic

Ver video

1) Efectuar las operaciones entre paréntesis, corchetes y llaves.

2 )Calcular las potencias y raíces.

3) Efectuar los productos y cocientes.

4) Realizar las sumas y restas.

POLINOMIOS ARITMÉTICOS. Ver estos dos videos: clic    clic

Un Polinomio es una expresión matemática conformada por un número limitado o finito de variables y constantes, entre las que se establecen operaciones aritméticas como la suma, la resta, multiplicación e incluso la potencia de números enteros.

Polinomios Aritméticos con signos de agrupación

Ver video: clic

En segundo lugar, resaltan aquellos Polinomios que sí cuentan con la presencia de signos de agrupación, como paréntesis, corchetes y llaves, así también como distintas operaciones aritméticas. De esta forma, un Polinomio Aritmético con signos de agrupación, bien podría expresarse de la siguiente forma:

52+ (4-2) – {34+ (2 x 3)-[38+24-(8+22) -8]+ 24}

Forma de resolver un Polinomio Aritmético con signos de agrupación  Ver video: Clic

En cuanto a la forma de resolver este tipo de expresiones matemáticas, sucederá igual que en las operaciones aritméticas en general. En este sentido, se seguirán los siguientes pasos:

• Operaciones que se encuentren dentro de paréntesis, las cuales también seguirán el orden de potencias y raíces, multiplicaciones y divisiones, sumas y restas.
• Acto seguido, se resolverán aquellas operaciones que se encuentren dentro de los corchetes, siguiendo el orden del primer punto.
• Así mismo, se solucionarán aquellas operaciones que se encuentren dentro de las llaves.
• Cuando ya no se cuenten con signos de agrupación, se procederán a resolver las potencias y raíces.
• Se continuará con las multiplicaciones y divisiones.
• Se resolverán las restas.
• Finalmente, se solucionarán las sumas, a fin de obtener la solución final.

Operaciones combinadas sin paréntesis

1) Combinación de sumas y restas:

Comenzando por la izquierda, vamos efectuando las operaciones según aparecen.

Ejemplo:

9 − 7 + 5 + 2 − 6 + 8 − 4 = 7

2) Combinación de sumas, restas y productos:

Realizamos primero los productos por tener mayor prioridad.

Posteriormente efectuamos las sumas y restas.

Ejemplo:

3 · 2 − 5 + 4 · 3 − 8 + 5 · 2 = 

= 6 − 5 + 12 − 8 + 10 = 15

3) Combinación de sumas, restas, productos y divisiones:

Realizamos los productos y cocientes en el orden en el que los encontramos porque las dos operaciones tienen la misma prioridad.

Efectuamos las sumas y restas.

Ejemplo:

10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 2 − 16 : 4 = 

5 + 15 + 4 − 10 − 8 + 8 − 4 =

5+ 15 + 4 +8 - 10 - 8 - 4 =

              32 - 22 = 10

4) Combinación de sumas, restas, productos , divisiones y potencias

Realizamos en primer lugar las potencias por tener mayor prioridad.

Seguimos con los productos y cocientes.

Efectuamos las sumas y restas.

Ejemplo:

2³ + 10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 2² − 16 : 4 = 

8   + 10 : 2    + 5 . 3 + 4 -  5 . 2 - 8 +  4 .  4 -   16 : 4 =

8  +  10 : 2  +  5 · 3  + 4 − 5 · 2 − 8 + 4 · 4 - 4   = 

8 +        5    +   15    + 4 −   10  − 8  +  16  − 4 = 

                               48 - 22 = 26

Ejemplo de operaciones combinadas

12 − {7 + 4 · 3 − [ ( (-2)² · 2 − 6)]}+ (2² + 6 − 5 · 3) + 3 − (5 − 2³: 2) =

12 − {7 + 4 · 3 − [(-2)² · 2 − 6)]}+ (2² + 6 − 5 · 3) + 3 − (5 − 2³: 2) =

1) Primero operamos con las potencias, productos y cocientes de los paréntesis.

Ejemplo:

= 12 − {7 + 4 · 3 −[ (4 · 2 − 6) ] } + (4 + 6 − 5 · 3) + 3 − (5 − 8 : 2) =

2) Operamos con los productos y cocientes de los paréntesis.

Ejemplo:

= 12 − {7 +12 − [ (8 − 6) ] } + (4 + 6 − 15) + 3 − (5 − 4) =

3) Realizamos las sumas y diferencias de los paréntesis.

Ejemplo:

= 12 − {7 + 12 − [ +2 ] } + (−5) + 3 − (+1) = 

= 12 − { 7 + 12  -   2  }    −   5   + 3   − 1 =

= 12 − { 7 + 12  -   2  }    −   5   + 3   − 1 =

= 12   -        17             -        5   + 3   - 1

=          15            -        23

=    - 8

4) La supresión de paréntesis ha de realizarse considerando que:

A) Si antes del paréntesis va el signo +, se quitará éste manteniendo su signo los términos que contenga. Ejemplo:

= 12 − (17 − 5 + 3 )− 1 = 

= 12  -   17 + 5  - 3  - 1=

=12   +  5   -  17  -  3  -  1=

=17    -    21=

=    -  4

B) Si antes del paréntesis va el signo −, al quitar el paréntesis hay que cambiar de signo a todo los términos que contenga.

Ejemplo:

= 12 + (17 − 5 + 3 )− 1 = 

= 12+17- 5 + 3 - 1=

=12+ 17 + 3 - 5 - 1=

=32  - 6=

=  26

Ver video antes de solucionar el taller: clic

video

TALLER N°1 

Tema : Polinomios y eliminación de signos de agrupación.

Resuelva los siguientes polinomios paso a paso, siguiendo el orden jerárquico para resolver operaciones: Este taller se adaptará a los tiempos y condiciones del grupo.

1)    -30+ {8 - [(-5)+1-5-(-3)]+(-7) } -  2³   

2)    - {2³+ ( -3 + 8:2) - [ 3 . 2 - 10 : (-5)] -9}

3)    - { 40 - [ 45 . 5 - ( 2³ +12) + 18  + 50] + ( - 35) }

4)       2²+ { -3 - [( 78-(-60-9)  . ( -2 . 3) ] + 98) } +  2³

5)   -1+2-{3-[5+7-(-9+10-11) -12+8 . 3]-  2³} 

6)    15-(-3+4)+{6 . 3+[2-5+7]- 2³-[-4+6-(-2+1+3)-6]}

7)    -{-4-5-15-[-2 . 9-10-(-8)-7+9]-16+7} + 2³

8)    -8-{-4+8-[7 . 6- 2³-(3+2-5)-(11+12)]-23}-37

9)     5+{-7-[6 . 5-12+(- 2³+15)]}-{-[-(-3+5+7)]}